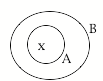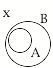Elements of Practical Reasoning

by Edward G. Rozycki

RETURN
edited 9/5/19

Uncovering Assumptions: Looking for a Method

Suppose someone were to say,

(A) Since this is only her first year on the job, Mary can’t be put in charge.

How would you argue against this? What assumptions are being made by the person who says it? Can you make these assumptions explicit?

Suppose now that someone tells you,

(B) If you want to get ahead, go to college!

What’s the reasoning behind this? Can you lay out the underlying argument and evaluate it? Even if you agree with the statement, can you strengthen it by strengthening its weakest assumptions? Or if you disagree with it, can you bring its weakest assumptions to the surface for examination?

Most people, by the time they reach adulthood, have developed an informal sense of “logic.” That is, they can more or less consciously -- if haphazardly -- “dope out” what went into the thinking of a person who presses for a particular point or proposes a specific undertaking. The point of this essay is to provide you with a means for consciously and methodically casting your “intuitions” into a common language -- and ancient, honored tradition -- which can be used to communicate your “intuitions” with others. In this way, you will discover how very much of a common species we are: human beings are a particular kind of reasoners. Our shared traits of intelligence are often obscured by the informal varieties of reasoning we normally encounter. This obscurity is often intensified by lack of training in a more formal manner of presentation.

The set of examples and exercises in this booklet will provide you with the means for analyzing informal arguments and evaluating them explicitly. The structure of the presentation is as follows:

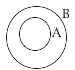
a. The first section assumes you have some acquaintance with Venn diagrams[1]. It demonstrates how to interpret them as statements involving implication, necessity and sufficiency.

b. The next two sections use Venn diagrams to define and illustrate the two basic argument forms, modus ponens and modus tollens.

c. Next we discuss the distinction between a valid argument and a sound argument and show how the two basic argument forms can be chained to create a complex argument.

d. Finally, we deal with enthymemes, the elliptical, compressed and apparently incomplete forms of argument that make up much of our day-to-day attempts to persuade each other to action. Precisely because we do not want to draw attention to our assumptions, we tend to explain ourselves in enthymemic form.

We will use our basic argument forms to help us reconstruct the reasoning underlying the enthymeme. This will make obvious -- and vulnerable -- the hidden premises of our enthymemic conclusion.

Interpreting Venn Diagrams as Argument Forms

Most of us have had some encounter with formal arguments, if only in our high school geometry course. Formal arguments are comprised of a list of premises from which follows, hopefully, something called a conclusion.

The problem is that hardly anyone attempts to persuade others by using formal arguments. Actual arguments appear to be more varied and complex than the forms we may have encountered in school.

We can deal with a great many informally stated arguments by working with only two argument forms. If you are familiar with Venn diagrams, the relationships that constitute valid, sound argument are easily represented by such diagrams.

In the charts below, each Venn diagram is given interpretations that enable them to illustrate argument forms.

Venn Diagram	Interpretation	Implication	Necessity & Sufficiency
1a.	All A is B Some B is A. e.g. All cats are animals.	A implies B B does not imply A.	A is sufficient for B B is necessary for A.
1b.	No A is B. No B is A. e.g. No dog is a chair.	A implies not-B B implies not-A.	A is neither necessary nor sufficient for B.
1c.	Some A is B. Some B is A. e.g. Some chairs are wood.	(no implications)	A is neither necessary nor sufficient for B.

It is important to note that implications are only possible for relationships 1a. and 1b. Such implications depend entirely upon terminological consensus. Reasoning depends upon implication, and implication only works to the extent to which consensus exists on how different terms relate to one another.

Modus Ponens

The first argument form is called modus ponens and is illustrated in the chart below.

Venn Diagram	Premisses and Conclusion	Alternative Form
2a.	A implies B, and x is in A; therefore x is in B. e.g. Every dog is a mammal, and Fido is a dog, therefore Fido is a mammal.	Let A = p. Let B = q, Restate the argument as p implies q p therefore q.

Tell what is wrong with this:

(C) Some animals are cold-blooded and Fido is an animal, so Fido is cold-blooded.

Can you illustrate the fallacy using Venn diagrams? This brings up an important point. A logical fallacy is made when a possible option (a conceivable situation) is dismissed out-of-hand. What possible option has been dismissed by (C)?

Modus Tollens

The only other argument form we need consider is called modus tollens. The chart below illustrates it.

Venn Diagram	Premisses and Conclusion	Alternative Form
2b.	A implies B, and x is not in B, So, x is not in A. e.g. Dogs are animals, and New York is not an animal, so New York is not a dog.	Let A = p Let B = q, then p implies q not q therefore not-p.

With just these two forms, modus ponens and modus tollens, we can reconstruct the arguments behind a good deal of informal reasoning. (Of course, there are subtleties we cannot deal with here, such as probabilistic reasoning, modal logics, problems with inconsistency and expressivity, etc. The interested reader is counseled to further study )

Soundness vs. Validity

Now we must observe a highly important distinction: that between a valid argument and a sound argument.

A valid argument, commonly called a “logical” argument is one which has the form of either modus ponens or modus tollens (or is a permissible combination or reiteration of any of the two -- see the next section.)

The reason we should be concerned that our arguments be valid is that invalid arguments prematurely dismiss possible options. Now, if our valid argument has true premisses -- and we may decide that they are true in a variety of ways this paper will not discuss -- the argument is not only valid, but sound. That is,

A sound argument is a valid argument with true premisses. The conclusion of a sound argument must be true.

We have a second important reason for constructing valid arguments: as long as our argument is valid, then, if our premisses can be demonstrated to be true -- by whatever means -- we can rest assured our conclusions are true. (Clearly, establishing premisses as true may be the bigger part of our task.)

It follows that even if the premisses of an argument are in doubt -- or even false -- the argument can be valid. This is extremely important. It means that we do not have to determine in advance the truth of our premisses to be assured we have not overlooked a conceivable possibility. Valid argument assures us that no necessary assumptions will remain hidden.

The following interrelationships between an argument’s validity and soundness exist:

•     an argument may be both valid and sound

•     an argument may be valid but not sound

•     an argument may be neither valid and nor sound

In the chart that follows examples of each are given showing an argument form (valid and invalid).with examples below.

1) Valid, sound (true premisses)	2) Valid, unsound (false premisses)	3) Invalid (despite true premisses and conclusion)	4) Invalid, (false premisses, true conclusion.
A implies B A therefore B	A implies B A therefore B	A implies B B therefore A	A implies B B therefore A
Any cat is a mammal. A Manx is a cat; therefore, a Manx is a mammal.	Any cat is a boat. A Manx is a cat; therefore, a Manx is a boat.	Any cat is a mammal. A Manx is a mammal; therefore, a Manx is a cat	Any cat is a canine. A Manx is a canine; therefore, a Manx is a cat.

We mentioned above that the trouble with invalid argument is that it hides conceivable possibility. Note that in the chart, 3) obscures the possibility that there are mammals that are not Manxes. This is why the truth of premisses alone, even when the truth of the conclusion has been ascertained, does not insure the validity of the argument. Truth without valid argument is at best good luck.

Combining for Longer Arguments

Above we defined a valid argument to be one with either a modus ponens or modus tollens form, or which combined or reiterated these forms. The simplest method is through chaining, where the conclusion of one argument becomes a premise for the next. The order of the premisses of a valid argument are not significant. Let’s look at some examples.

modus ponens chain (compressed)	modus ponens-modus tollens chain (compressed)
A implies B B implies C A therefore C.	A implies B C implies not-B A therefore not-C
Any wolf is a canine. Any canine is a mammal therefore any wolf is a mammal.	Any dog is a canine. A feline is not a canine. A beagle is a dog. therefore a beagle is not a feline.

Can you decompress the examples given above? (Hint: write each one as two arguments in sequence.)

Enthymemes

Finally, we get to the point of the previous exercises and discussion: to examine forms of argument where premisses have been hidden. Consider again,

(A) Since this is only her first year on the job, Mary can’t be put in charge.

The way we will proceed is to

1) Treat this claim as the conclusion of an argument.

2) Assume that a valid argument form underlies this claim.

3) Reconstruct plausible premisses which together with the conclusion form a valid argument.

Since modus ponens is the easiest form to deal with, let’s try this:

a. First year people can’t be put in charge.

b. Mary is a first year person.

c.Therefore, Mary can’t be put in charge.

This is simple enough, perhaps too simple, since if you challenge the conclusion, the person advocating it will probably show more ingenuity than our reconstruction indicates.

Let’s try something a little more complex, yet more realistic.

a. First year people have insufficient experience for leadership positions.

b. Putting someone in charge, even temporarily, is a leadership position.

c. Mary is a first year employee.

d. Therefore, Mary cannot be put in charge.

Basically what is being said here is that experience is necessary to leadership, that is leadership (L) implies experience (E)

(L) implies (E).

Also, first year people (F) do not have experience (E), that is

F implies not E.

We see obviously that Mary (M) is a first year person(F)

M implies F (or M is an F, it works the same) and

being put in charge (P) is a case of leadership (L),

P implies L,

so if we look at the formulas we recognize a combination of modus ponens and modus tollens underlying the enthymeme.

L implies E.

F implies not E.

M implies F

P implies L,

If we rearrange these and group them we see what’s up:

Part A:

M implies F

F implies not E.

Clearly, Mary, being a first year person, has no experience. Let’s continue:

Part B:

P implies L,

L implies E.

That is , being put in charge, a leadership position, requires experience., i.e. P implies E.

But by part A, not-E, that is Mary has no experience. Therefore by modus tollens,

not-P.

This may seem a roundabout way to explain what possibly went on in someone’s head when they announced A). But unless someone could justify it in such a manner, the decision it announces would be considered whimsical, arbritrary, unreasoned. On the other hand, our analysis enables us to identify the assumptions underlying the judgment so as to bring them up for questioning.

(Can you give a similar analysis for

(B) If you want to get ahead, go to college!)

Where do we go from here? It depends upon what we want to do. Notice, for example. the some of the premises are slogans. We might want to criticize them as obscuring important distinctions or imputing false causes.[2] Or, rather than criticize, we might want to reconstruct the argument using different premises so as to make the conclusion stronger. The analysis we have just completed is a preparatory step to other undertakings. [3]

Other examples for analysis

(D) Sam can’t write curriculum for Black Studies; he’s Puerto Rican.

(E) Federal money has to be spent to serve everyone, not just a religious sect.

(F) Your students won’t improve unless you raise your expectations.

(G) Gun control will reduce violent crime.

(H) How can we be surprised about violence in the schools considering how much violence there is on TV?

(I) Show me a school with problems and I’ll show you one lacking leadership!

(J) Only when humankind finally gets serious about peace will wars stop.

(K) Since real education involves our deepest values, we might as well close down all non-religious schools.

(L) Because so many kids today lack direction, our schools must incorporate Values Education into the curriculum.